近期,苏州大学蒋建华教授课题组与南京大学卢明辉教授、陈延峰教授课题组合作在高阶拓扑物理领域再次取得重要进展。蒋建华教授首先在理论上提出了一种受非点群对称性保护的新型多级拓扑绝缘体,其不同带隙可以分别支持偶极子和四极子极化,相应地表现出声学类自旋霍尔效应和异常声二阶拓扑现象。在实验方面,南大合作者通过3D打印技术以及相关声波扫场技术,验证了理论预言的相关拓扑效应。文章以“Symmetry-protected hierarchy of anomalous multipole topological band gaps in nonsymmorphic metacrystals”为题发表于近期的Nature Communication。

非点群对称性主要包含了滑移对称性及螺旋对称性,其对称操作由旋转(或镜面)及平移符合而成。在实现经典拓扑波动系统方面,非点群对称性扮演着重要的角色。通过在经典波动系统中引入非点群对称性,蒋建华教授课题组在相关领域已发表多篇高水平研究论文。例如,他们在光学系统中实现了第II型的Dirac点,并揭示一系列奇异的光学折射效应[npj Quantum Materials 2, 54 (2017)];在弹性波系统中实现了由对称性导致必然存在的拓扑节线[Phys. Rev. B 97, 180101 (2018)];在表面波光子晶体中实现了高阶拓扑态[Adv. Sci. 7, 1902724 (2019)];在声学系统实现了多维度二阶拓扑绝缘体以及三维层级高阶拓扑绝缘体[Nat. Phys. 15, 582-588 (2019), Nat. Commun. 10, 1(2019)]。
在此项工作中,他们研究的目标是实现由四极子极化导致的高阶拓扑绝缘体。根据电子系统的紧束缚模型,这种高阶拓扑绝缘体需要实现不同格点之间正负耦合系数,这为实验实现增加了难度。蒋建华课题组发挥自身优势,另辟蹊径,设计了一种具有滑移对称性的正方晶格声子晶体,其周期单元含四个直角拱形散射体(如图1所示),通过调节散射体的结构参数实现晶体对称性的变化,从而触发系统的高阶拓扑相变(如图2所示)。研究发现,第二带隙具有非零的四极子极化参数,其量子化由滑移对称性保证,揭示了一类由对称性保护的四极子拓扑绝缘体。
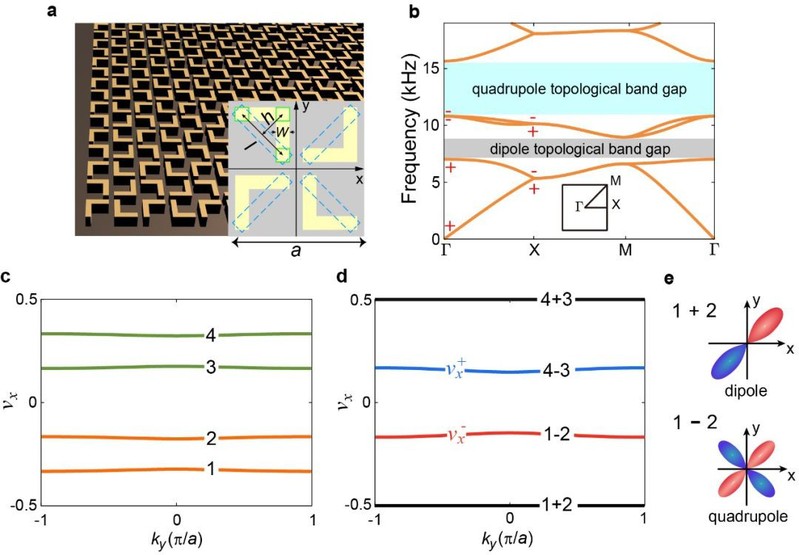
图一 非点群声子晶体中受对称性保护的多级拓相
进一步计算结果显示,当结构具有p4g空间群对称性时,其表现出四极子拓扑绝缘体特有的性质,即体带隙中拥有带带隙的边界态和处于边界态带隙中的角态;经过几何相变,体带隙闭合、角态消失;当结构经过几何相变之后具有C4v点群对称性,即便再次打开带隙,带隙中原本由于四极子导致的角态也不再出现,证明几何相变正对应于四极子的拓扑相变,经过拓扑相变,四极子极化消失。由于工作在不同的带隙中(对应于不同的频率)实现不同的拓扑现象,有望在多路复用声传播和声波调制中产生应用。
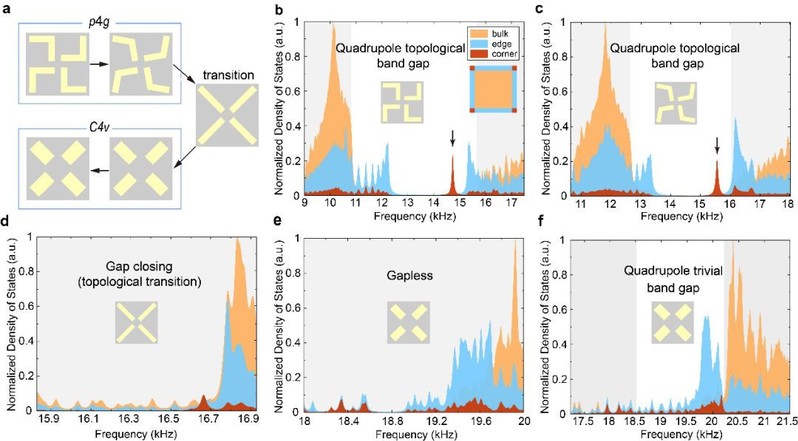
图二 第二带隙中的四极子拓扑相变
该项研究得到了国家自然科学基金、江苏省特聘教授等项目的资助支持。


